Convolution is a widely used technique in image and signal processing applications. In image processing the convolution operator is used as a filter to change the characteristics of the image; sharpen the edges, blur the image or remove the high or low frequency noise. In seismic processing a convolution can be used to extrapolate the propagating wavefield forward of backward. In signal processing it can be used to suppress unwanted portions of the signal or separate the signal in different parts.
Two dimensional (2D) convolutions are sometimes the most time consuming parts of an application. It is therefore useful to consider different implementations of a 2D convolution and compare the performance.
In this article the algorithm for a position dependent symmetric 2D convolution operator is discussed. Four implementation, for complex valued operators and data, are discussed and compared with each other. The performance of these algorithms is shown on both Intel and MIPS processors.
A 2D convolution is represented by:
| (1) |
The convolution operator discussed in this article will be dependent on its spatial position and in that case the Fourier transformation cannot be used. This means that the convolution must be done in the spatial domain. An example of this can be found in seismic processing where a wavefield extrapolation method can be implemented as a 2D convolution. In this wavefield extrapolation method the convolution operator is a wavefield propagation operator W which extrapolates the known wavefield P at depth level zm to the wavefield P at depth level zm+1. The spatial convolution operator can be different for every spatial position, because the propagation velocity of the medium can be different.
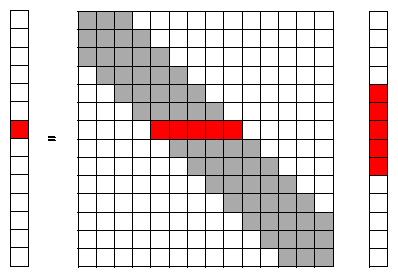
Since we are using a numerical solution with finite boundaries it is more convenient to replace the integral of equation (1) with a matrix-vector equation. To make the problem easier to explain a 1 dimensional convolution is used with a convolution operator of 3-points:
| (2) |
In this equation the W matrix represent the convolution operator and the P vector the data. For a symmetric operator W(-1) equals W(1) and using this symmetry in the implementation can be very beneficial for the performance.
Depending on the type of symmetry in the operator there are many other methods to implement a symmetric 2D convolution. By making appropriate assumptions about the spatial variations of the operator, which depends on the data it is applied to, it is possible to perform the convolution in the Fourier domain (which is fast) and do a small correction for the variations. These methods can give very good results and are usually faster than the 2D convolution discussed here. However, the 2D convolution is the method with only one minor approximation (it assumes that there is no variation within the operator stencil) and can be used in many different problems.
Four algorithms, ranging from the most simple implementation to an advanced implementation which is optimized for cache re-usage, are discussed. In short a 2 dimensional convolution is simple a 4 nested loop. In all code fragments oplx, oply are the operator lengths in x and y direction nx, ny are the data dimensions. The opx array contains the convolution operator and the data array contain the data. velmod is a 2D array which contains information weather a new operator has to be loaded or not. If the velmod array has a different value than the previous operator used (c) a new operator has to be loaded. These operators are stored in a table and readtable2D gets the correct operator given the value of c and om.
The most simple implementation does not make use of the symmetry in the operator and loops over all x and y positions and does the convolution over the complete operator length (oplx x oply points). Note that there is some logic added in the loops to take care of the boundaries of the data array.
hoplx = (oplx+1)/2;
hoply = (oply+1)/2;
for (iy = 0; iy < ny; iy++) {
starty = MAX(iy-hoply+1, 0);
endy = MIN(iy+hoply, ny);
for (ix = 0; ix < nx; ix++) {
startx = MAX(ix-hoplx+1, 0);
endx = MIN(ix+hoplx, nx);
/* if velocity changes calculate new operator */
if (velmod[iy*nx+ix] != c) {
c = velmod[iy*nx+ix];
readtable2D(opx, om/c, hoplx, hoply, mode);
}
/* convolution with the operator */
dumr = dumi = 0.0;
k = MAX(hoply-1-iy, 0);
for (i = starty; i < endy; i++) {
l = MAX(hoplx-1-ix, 0);
for (j = startx; j < endx; j++) {
dumr += data[i*nx+j].r*opx[k*oplx+l].r;
dumr += data[i*nx+j].i*opx[k*oplx+l].i;
dumi += data[i*nx+j].i*opx[k*oplx+l].r;
dumi -= data[i*nx+j].r*opx[k*oplx+l].i;
l++;
}
k++;
}
convr[iy*nx+ix].r = dumr;
convr[iy*nx+ix].i = dumi;
}
}
The algorithm shown below makes use of the 2D symmetry in the operator. It first sums the 4 quarters of the data together and then does the convolution over (oplx/)-1 x (oply/2)-1 points, which is 1/4 of the full operator size. This algorithm requires less multiplication as the previous algorithm. To avoid the calculations of the boundaries the data is copied into an array with the dimension nxo x nyo. Where nxo is the original datasize + the operator length-1.
hx2 = hoplx-1;
hy2 = hoply-1;
nxo = nx+2*hx2;
nyo = ny+2*hy2;
for (iy = 0; iy < ny; iy++) {
memcpy(&term1[(iy+hy2)*nxo+hx2], &data[iy*nx], nx*sizeof(complex));
}
for (iy = hy2; iy < nyo-hy2; iy++) {
pos = (iy-hy2)*nx-hx2;
for (ix = hx2; ix < nxo-hx2; ix++) {
/* First make use of symmetry in x and y axis */
quart[0] = term1[iy*nxo+ix];
for (i = 1; i < hoply; i++) {
for (j = 1; j < hoplx; j++) {
quart[i*hoplx+j].r = (term1[(iy-i)*nxo+ix-j].r +
term1[(iy+i)*nxo+ix-j].r +
term1[(iy-i)*nxo+ix+j].r +
term1[(iy+i)*nxo+ix+j].r);
quart[i*hoplx+j].i = (term1[(iy-i)*nxo+ix-j].i +
term1[(iy+i)*nxo+ix-j].i +
term1[(iy-i)*nxo+ix+j].i +
term1[(iy+i)*nxo+ix+j].i);
}
}
for (j = 1; j < hoplx; j++) {
quart[j].r = (term1[iy*nxo+ix-j].r +
term1[iy*nxo+ix+j].r );
quart[j].i = (term1[iy*nxo+ix-j].i +
term1[iy*nxo+ix+j].i );
}
/* if velocity changes calculate new operator */
if (velmod[pos+ix] != c) {
c = velmod[pos+ix];
readtable2D(hopx, om/c, hoplx, hoply, mode);
}
/* convolution with the operator */
dumr = 0.0;
dumi = 0.0;
for (i = 0; i < hoply; i++) {
for (j = 0; j < hoplx; j++) {
dumr += quart[i*hoplx+j].r*hopx[i*hoplx+j].r;
dumr += quart[i*hoplx+j].i*hopx[i*hoplx+j].i;
dumi += quart[i*hoplx+j].i*hopx[i*hoplx+j].r;
dumi -= quart[i*hoplx+j].r*hopx[i*hoplx+j].i;
}
}
data[pos+ix].r = dumr;
data[pos+ix].i = dumi;
}
}
If the operator is circle symmetric we can reduce the number of operations even more. The convolution is now done over 1/8 of the size of the operator. The inner loop index of the convolution has become dependent on the value of the outer loop. This means that loop unrolling cannot be done very efficiently by the compiler. To get the best performance for this type of symmetry the user should do the loop unrolling by-hand for the most common sizes of the operator. So he should should make a function for the 25x25 operator another one for the 19x19 operator, and so on....
hoplx = (oplx+1)/2;
hoply = (oply+1)/2;
hx2 = hoplx-1;
hy2 = hoply-1;
nxo = nx+2*hx2;
nyo = ny+2*hy2;
term1 = (complex *)calloc(nxo*nyo, sizeof(complex));
oct = (complex *)malloc(hoplx*hoply*sizeof(complex));
hopx = (complex *)malloc(hoplx*hoply*sizeof(complex));
for (iy = 0; iy < ny; iy++) {
memcpy(&term1[(iy+hy2)*nxo+hx2], &data[iy*nx], nx*sizeof(complex));
}
for (iy = hy2; iy < nyo-hy2; iy++) {
pos = (iy-hy2)*nx;
for (ix = hx2; ix < nxo-hx2; ix++) {
/* First make use of symmetry in x and y axis */
oct[0] = term1[iy*nxo+ix];
for (i = 2; i < hoply; i++) {
for (j = 1; j < i; j++) {
oct[i*hoplx+j].r =
term1[(iy+i)*nxo+ix+j].r + term1[(iy+i)*nxo+ix-j].r +
term1[(iy-i)*nxo+ix+j].r + term1[(iy-i)*nxo+ix-j].r +
term1[(iy+j)*nxo+ix+i].r + term1[(iy+j)*nxo+ix-i].r +
term1[(iy-j)*nxo+ix-i].r + term1[(iy-j)*nxo+ix+i].r;
oct[i*hoplx+j].i =
term1[(iy+i)*nxo+ix+j].i + term1[(iy+i)*nxo+ix-j].i +
term1[(iy-i)*nxo+ix+j].i + term1[(iy-i)*nxo+ix-j].i +
term1[(iy+j)*nxo+ix+i].i + term1[(iy+j)*nxo+ix-i].i +
term1[(iy-j)*nxo+ix-i].i + term1[(iy-j)*nxo+ix+i].i;
}
}
/* Second make use of the diagonal symmetry (only if dx == dy) */
for (i = 1; i < hoply; i++) {
oct[i*hoplx].r = (term1[(iy-i)*nxo+ix].r +
term1[iy*nxo+ix-i].r +
term1[(iy+i)*nxo+ix].r +
term1[iy*nxo+ix+i].r);
oct[i*hoplx].i = (term1[(iy-i)*nxo+ix].i +
term1[iy*nxo+ix-i].i +
term1[(iy+i)*nxo+ix].i +
term1[iy*nxo+ix+i].i);
oct[i*hoplx+i].r = (term1[(iy-i)*nxo+ix-i].r +
term1[(iy+i)*nxo+ix-i].r +
term1[(iy-i)*nxo+ix+i].r +
term1[(iy+i)*nxo+ix+i].r);
oct[i*hoplx+i].i = (term1[(iy-i)*nxo+ix-i].i +
term1[(iy+i)*nxo+ix-i].i +
term1[(iy-i)*nxo+ix+i].i +
term1[(iy+i)*nxo+ix+i].i);
}
/* if velocity changes calculate new operator */
if (velmod[pos+ix-hx2] != c) {
c = velmod[pos+ix-hx2];
readtable2D(hopx, om/c, hoplx, hoply, mode);
}
/* convolution with the operator */
dumr = 0.0;
dumi = 0.0;
for (i = 0; i < hoply; i++) {
for (j = 0; j <= i; j++) {
dumr += oct[i*hoplx+j].r*hopx[i*hoplx+j].r;
dumr += oct[i*hoplx+j].i*hopx[i*hoplx+j].i;
dumi += oct[i*hoplx+j].i*hopx[i*hoplx+j].r;
dumi -= oct[i*hoplx+j].r*hopx[i*hoplx+j].i;
}
}
data[pos+ix-hx2].r = dumr;
data[pos+ix-hx2].i = dumi;
}
}
All previous implementation did not care about the cache and only made use of the symmetry in the operator. The method shown below tries to reuse the data in the cache as good as possible and also make use on the symmetry in the x and y direction. This method arranges the data in such a way that in the inner loop (of length opersize = (oplx x oply) ) only stride one access is needed. To get the data in this shape the additions done in the x directions are stored in the tmp3 array. The tmp4 array is equal to the tmp3 array with the y index reversed. Note that the values in the tmp3 array are reused over the total length.
hoplx = (oplx+1)/2;
hoply = (oply+1)/2;
hoplx2 = hoplx-1;
hoply2 = hoply-1;
lenx = nx+2*hoplx2;
leny = ny+2*hoply2;
tmpsize = leny*hoplx+nx;
opersize = hoplx*hoply;
copy = (complex *)calloc(lenx*leny, sizeof(complex));
tmp3 = (complex *)calloc(tmpsize, sizeof(complex));
tmp4 = (complex *)calloc(tmpsize, sizeof(complex));
hopx = (complex *)calloc(opersize, sizeof(complex));
/* Copy data into another array with zeroes added to the edges */
for (iy = 0; iy < ny; iy++) {
memcpy(©[(hoply2+iy)*lenx+hoplx2], &data[iy*nx],
nx*sizeof(complex));
}
memset( (float *)&data[0].r, 0, 2*nx*ny*sizeof(float) );
/* fill temporary arrays */
for (iy = 0; iy < leny; iy++) {
for (ix = 0; ix < hoplx; ix++) {
tmp3[iy*hoplx+ix].r = copy[iy*lenx+hoplx2+ix].r +
copy[iy*lenx+hoplx2-ix].r;
tmp3[iy*hoplx+ix].i = copy[iy*lenx+hoplx2+ix].i +
copy[iy*lenx+hoplx2-ix].i;
}
}
fiy = 0; iy < leny; iy++) {
memcpy(&tmp4[iy*hoplx], &tmp3[(leny-iy-1)*hoplx],
hoplx*sizeof(complex));
}
/* The 2D-Convolution */
for (ix = 0; ix < nx; ix++) {
for (iy = 0; iy < ny; iy++) {
pos = iy*nx+ix;
/* if velocity changes calculate new operator */
if (velmod[pos] != c) {
c = velmod[pos];
readtable2D(hopx, om/c, hoplx, hoply, mode);
}
index3 = (hoply2+iy)*hoplx;
index4 = (leny-hoply2-iy-1)*hoplx;
datar = datai = 0.0;
for (j = 0; j < opersize; j++) {
dumr = tmp3[index3+j].r + tmp4[index4+j].r;
dumi = tmp3[index3+j].i + tmp4[index4+j].i;
datar += dumr*hopx[j].r;
datar += dumi*hopx[j].i;
datai += dumi*hopx[j].r;
datai -= dumr*hopx[j].i;
}
data[pos].r = datar;
data[pos].i = datai;
}
for (iy2 = 0; iy2 < leny; iy2++) {
for (ix2 = 0; ix2 < hoplx; ix2++) {
tmp3[iy2*hoplx+ix2].r = copy[iy2*lenx+hoplx2+ix2+ix].r +
copy[iy2*lenx+hoplx2-ix2+ix].r;
tmp3[iy2*hoplx+ix2].i = copy[iy2*lenx+hoplx2+ix2+ix].i +
copy[iy2*lenx+hoplx2-ix2+ix].i;
}
}
for (iy2 = 0; iy2 < leny; iy2++) {
memcpy(&tmp4[iy2*hoplx], &tmp3[(leny-iy2-1)*hoplx],
hoplx*sizeof(complex));
}
}
The convolution stencil in the performance test is circular symmetric and has a full size of 25x25 points (oplx=25 and oply=25). In the tables below the size of the area is indicated with 201, 501, 1001, 2501: meaning a size of 201x201 (nx x ny), .... points.
| Method | Size | O2000 | O3000 | SGI 1400 | SGI 1200 |
| simple | 201 | 5.4 | 4.1 | 13.3 | 10.2 |
| Q4 | 201 | 5.8 | 4.3 | 10.0 | 6.9 |
| Q8 | 201 | 4.7 | 3.5 | 9.0 | 6.0 |
| cache | 201 | 2.6 | 2.0 | 5.0 | 4.4 |
| simple | 501 | 34.8 | 26.3 | 91.0 | 67.7 |
| Q4 | 501 | 35.6 | 26.7 | 63.7 | 44.3 |
| Q8 | 501 | 28.8 | 21.5 | 57.9 | 38.5 |
| cache | 501 | 16.6 | 12.7 | 31.6 | 30.1 |
| simple | 1001 | 142.0 | 107.2 | 353.4 | 269.7 |
| Q4 | 1001 | 159.8 | 119.5 | 285.7 | 192.0 |
| Q8 | 1001 | 153.6 | 114.4 | 277.0 | 174.3 |
| cache | 1001 | 69.6 | 52.3 | 124.9 | 130.8 |
| simple | 2501 | 937.6 | 702.5 | 2222.4 | 2222.4 |
| Q4 | 2501 | 898.8 | 669.7 | 1549.3 | 1549.3 |
| Q8 | 2501 | 731.2 | 541.0 | 1406.2 | 1406.2 |
| cache | 2501 | 467.1 | 351.4 | 811.2 | 863.9 |
The O2000 has 300 MHz R12000 with 8 MB L2-cache running at 200 MHz. O3000 with 400 MHz R12000 processors and a 8 MB L2-cache running at 266 MHz. SGI 1400 has Pentium III (Katmai) processors running at 500 MHz with 2 MB L2-cache. and the gcc compilers have been used. SGI 1200 has PIII (Coppermine) CPU's running at 700 MHz and compiled with the Portland Group compilers. The notation Q4 stands for the 2D symmetric method and Q8 is the circle symmetric method.
The size of one 201x201 slice is 316 KB which easily fits in the L2-cache, but not in the L1-cache. The 501x501 slice is 2 MB, 1001x1001 7.6 MB and 2501x2501 47 MB.
For the 501 size a more detailed analysis has been done for the 300 MHz R12K (with a peak performance of 600 Mflop/s). In this table the different resources used by the different methods becomes clear. The number of floating point operations (Mflop column) is the highest for the simple method and the lowest for the cachea and Q8 method.
| Method | MFlops | Mflop/s | 109Inst. | Bandwidth |
| simple | 18726 | 538 | 24.8 | 0.4 |
| Q4 | 9563 | 275 | 22.2 | 2.2 |
| Q8 | 6901 | 239 | 20.0 | 1.3 |
| cache | 6492 | 391 | 11.3 | 3.9 |
The bandwidth column is the used memory bandwidth from the perfex profile (see man perfex for more information on this command). The low values (1-3 MB/s range) indicate that the bandwidth is not used and that most data is in the L2-cache of the R12K. For the 'cache' method and size 1001 the memory bandwidth used is 14.8 MB/s and for size 2500 the bandwidth used is 24.8 MB/s.
The most simple implementation has a very high Mflop/s rate, but it is not the fastest implementation because it uses many floating point operations to calculate the result. Using the symmetry in the operator can be very beneficial if the re-usage of the cache is taken into account.
The source code can be downloaded from: extr3D.tar.gz
This file in PDF format 2DConvolution.pdf
Useful links about 2D convolution are:
A good reference book is:
Signals and Systems, Second Edition Alan V. Oppenheim, Alan S. Willsky, S. Nawab Nawab, Syed ham Nawab, Prentice Hall, Hardcover, 2nd edition, Published August 1996, 960 pages, ISBN 0138147574