In homogeneous media the one-way extrapolation operator in the kx-w (wavenumber-frequency) domain is a simple analytical function. The advantage of computation in the kx-w domain is that the desired result is obtained by multiplication of the data with the operator. But simple multiplication in the kx-w domain rules out the possibility of applying a laterally varying operator. Another disadvantage is the numerical artefact in x due to undersampling in kx. To allow laterally varying medium functions and less numerical artefacts a convolutional operator in the x-w (space-frequency) domain should be used. When the spatial extrapolation operator is used in an explicit recursive depth migration algorithm it must be calculated in an optimum way to obtain reliable and stable results. There are several ways to obtain a spatial convolution operator. For homogeneous media one usually starts with the exact analytical expression in the kx-w domain and transforms this operator back to the spatial domain. In recent years many methods have been developed to do this transformation in an efficient and optimum way. For the one-way extrapolation operator Holberg (1988), Blacquiere (1989), Hale (1990) and Nautiyal et al. (1993) have proposed methods to arrive at spatial operators which are unconditionally stable in a recursive extrapolation scheme. In DELPHI Volume IV, Appendix D (1993) an alternative method is presented for an efficient and controlled transformation back to the spatial domain. This method can be used to calculate extrapolation operators which should be stable and accurate in a recursive depth migration algorithm. First some examples of extrapolation operators for homogeneous media are given. The theoretical derivation for the proposed numerical optimization scheme was already given in Appendix D of the DELPHI Volume IV (1993). The proposed method is compared with other numerical optimization methods and finally some results of recursive depth migration, in acoustic media with the optimized extrapolation operators, are given in DELPHI Volume V, Appendix A.
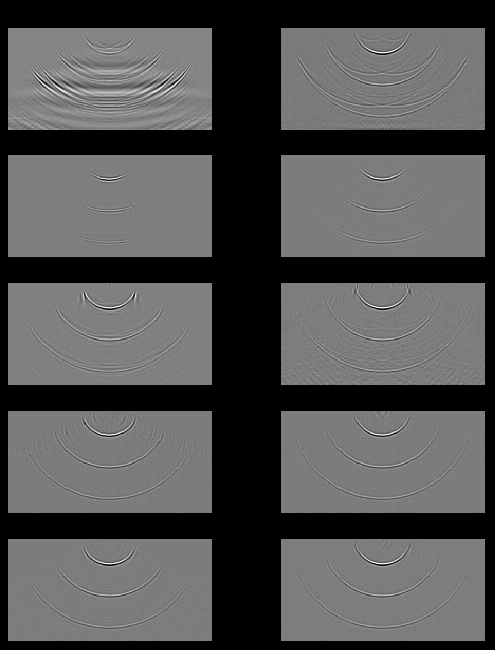
The operators obtained with the weighted least square optimization procedure are economic, stable and accurate. Reducing the operator length will decrease the computation time, but for very short operators the steep dip will become inaccurate and unstable. Comparing the weighted least square operators with the computationally intensive non-linear optimized operators, it may be concluded that only a small difference occurs at the high angles: the weighted least squares operator decays a little in amplitude while the non-linear operators keep the amplitude correct (although they give rise to small artefacts at the high angles). In the DELPHI project we have chosen for the weighted least squares method to compute the operator table, because of its stable and accurate behaviour for a broad range of operators and the relatively small computation time. The weight function used in the optimization procedure can also be optimized in order to give the spatial operator an even more controlled behavior. This optimization of the weight function is a topic for future research. The length of the optimized operator is for a certain error a function of the wavenumber. In calculating the table of operators this length dependency could be taken into account to arrive at an even more efficient extrapolation. At the moment we are also investigating a similar optimization process for 3D operators.
2D extrapolation operator optimization (EAEG94)
3-D recursive extrapolation operators: an overview (SEG94)
3D extrapolation operator optimization (EAEG95)
3D
recursive extrapolation operators